Démineur

Démineur

Rappelons brièvement les principes du jeu : explorer un champ de mines sans marcher sur l'une d'elles.
Un champ de mines est un tableau à deux dimensions dont quelques cases contiennent des mines cachées alors que les autres sont vides. En début de partie toutes les cases sont recouvertes et le joueur doit les découvrir l'une après l'autre. Le joueur est victorieux quand il a réussi à découvrir toutes les cases ne contenant pas de mines.

À chaque étape du jeu, le joueur peut au choix ouvrir une case, ou la marquer comme minée. S'il ouvre une case et que celle-ci contient une mine, il saute et perd la partie. Sinon, la case change d'aspect et s'y inscrit le nombre des cases adjacentes qui sont minées (donc au maximum 8). S'il choisit de marquer la case, il ne peut plus ensuite l'ouvrir sans avoir au préalable retiré la marque.

Figure 6.5 : Copie d'écran

Nous décomposons l'implantation de ce jeu en trois parties.

La description d'un jeu abstrait comprenant la représentation interne du champ de mines et les fonctions manipulant cette représentation.
La description graphique du jeu avec ses fonctions propres pour le rendu de l'affichage des cases.
Le moteur gérant les interactions entre le programme et l'utilisateur.

Le champ de mines abstrait

Cette partie ne s'intéresse qu'au champ de mines considéré comme une pure abstraction, nous ne nous occupons pas de son affichage.

Configuration

Un champ de mines est caractérisé par ses dimensions et le nombre de mines qu'il contient. Nous regroupons ces trois paramètres dans un enregistrement et définissons une configuration par défaut : 10×10 cases et 15 mines.


# type config = { 
   nbcols  : int ;
   nbrows : int ; 
   nbmines : int };;
# let default_config = { nbcols=10; nbrows=10; nbmines=15 } ;;

Le champ de mines

Il apparaît naturel qu'un champ de mines soit codé par un tableau à deux dimensions. Il nous faut encore préciser ce que sont ces cases en déterminant les informations qu'il est nécessaire de connaître pour chacune d'elle. L'état d'une case peut être :

la case est-elle minée ?
la case a-t-elle été découverte ?
la case a-t-elle été marquée ?
combien y a-t-il de cases minées parmi les cases adjacentes ?

Cette dernière information n'est pas indispensable puisqu'il est possible de la calculer au moment opportun, mais il est plus simple de faire ce calcul une fois pour toutes en début de partie.

Nous représentons une case par un enregistrement contenant ces quatre informations.


# type cell = { 
   mutable mined : bool ;
   mutable seen : bool ; 
   mutable flag : bool ; 
   mutable nbm : int     
 } ;;

Le tableau à deux dimensions du champ de mine est un tableau de tableaux de cases :


# type board = cell array array  ;;

Un itérateur

Dans la suite du programme nous aurons à de multiples occasions besoin d'appliquer une fonction à chacune des cases du champ de mines. Pour le faire génériquement, nous définissons l'itérateur iter_on_cell appliquant la fonction f donnée en argument à chaque case du tableau défini par la configuration cf.


# let iter_on_cell cf f = 
   for i=0 to cf.nbcols-1 do for j=0 to cf.nbrows-1 do f (i,j) done done ;;
val iter_on_cell : config -> (int * int -> 'a) -> unit = <fun>

Nous avons ici un bon exemple du mélange des styles fonctionnel et impératif, puisque pour itérer une fonction opérant par effet de bord (puisque sans résultat) sur toutes les coordonnées d'un tableau nous utilisons une fonctionnelle (une fonction prenant en argument une autre fonction).

Initialisation

Nous déterminons aléatoirement l'ensemble des cases minées. Si l et c sont respectivement le nombre de lignes et le nombre de colonnes du champ de mines et m le nombre de mines, il faut engendrer une liste de m nombres différents compris entre 1 et l× c. On supposera que m£ l× c pour définir l'algorithme, mais le programme devra explicitement vérifier cette condition.

L'idée la plus naturelle et la plus simple est de commencer avec une liste vide, de tirer un nombre au hasard, de l'introduire dans la liste s'il n'y apparaît pas déjà; et de recommencer jusqu'à ce que la liste contienne m nombres. Pour cela nous utiliserons les fonctions suivantes prises dans les modules Random et Sys :

Random.int : int -> int qui tire selon un générateur de nombres aléatoires un nombre compris entre 0 et n-1 si n est l'argument passé ;
Random.init : int -> unit, qui initialise le générateur de nombres aléatoires ;
Sys.time : unit -> float, qui retourne le nombre de millisecondes de temps processeur utilisé depuis le début de l'exécution du programme. Cette fonction sera utilisée pour initialiser le générateur de nombres aléatoires de manière différente à chaque partie.

Les modules auxquels appartiennent ces fonctions sont détaillés au chapitre 8, pages ?? et ??.

La fonction de tirage aléatoire des mines prend en argument le nombre de cases (lc) ainsi que le nombre de mines à tirer (m) et retourne une liste de positions linéarisées des m mines.


# let random_list_mines lc m = 
   let cell_list = ref [] 
   in while (List.length !cell_list) < m do 
        let n = Random.int lc in
         if not (List.mem n !cell_list) then cell_list := n :: !cell_list 
      done ;
     !cell_list ;;
val random_list_mines : int -> int -> int list = <fun>

Telle qu'elle est écrite, nous ne sommes pas capable de dire en combien d'étapes cette fonction se termine. Si notre générateur aléatoire est fiable, nous pouvons uniquement assurer que la probabilité qu'elle ne termine pas est nulle. Ce qui nous donne la proposition paradoxale : << la fonction termine si elle tourne infiniment >>.
Cependant, la pratique n'a jamais mis en défaut notre fonction. Aussi nous contenterons nous de cette définition incertaine pour engendrer la liste des cases minées.

Il nous faut initialiser le générateur de nombres aléatoires pour que chaque exécution du jeu ne se fasse pas avec le même champ de mines. On utilise le temps processeur depuis le début de l'exécution du programme pour initialiser le générateur de nombres aléatoires.


# let generate_seed () =
   let t = Sys.time () in           
   let n = int_of_float (t*.1000.0) 
   in Random.init(n mod 100000) ;;           
val generate_seed : unit -> unit = <fun>

Dans la pratique on s'aperçoit qu'un même programme prendra souvent le même temps d'exécution ce qui entraîne un tirage unique de la fonction generate_seed. On utilisera de préférence la fonction Unix.time (voir chapitre 18).

Aussi bien lors de l'initialisation du champ de mines que lors du jeu, nous aurons besoin de connaître l'ensemble des cases adjacentes à une case donnée (fonction neighbours). L'énumération de cet ensemble doit prendre en compte les cases des bords qui ont moins de voisins que celles du milieu du jeu (fonction valid).


# let valid cf (i,j) = i>=0 && i<cf.nbcols && j>=0 && j<cf.nbrows  ;;
val valid : config -> int * int -> bool = <fun>
# let neighbours cf (x,y) =
   let ngb = [x-1,y-1; x-1,y; x-1,y+1; x,y-1; x,y+1; x+1,y-1; x+1,y; x+1,y+1]
   in List.filter (valid cf) ngb ;;
val neighbours : config -> int * int -> (int * int) list = <fun>

La fonction initialize_board crée le champ de mines initial. Elle procède en quatre étapes :

génération de la liste des cases minées;
création d'un tableau à deux dimensions contenant des cellules différentes;
marquage des cases minées;
décompte des cases minées adjacentes à chaque case non minée.

La fonction initialize_board utilise un certain nombre de fonctions locales que nous décrivons brièvement.

cell_init: : crée une valeur initiale ;
copy_cell_init: : affecte une case du tableau avec une nouvelle copie de la valeur initiale ;
set_mined: : dépose une mine dans une case ;
count_mined_adj: : compte le nombre de cases minées adjacentes à une case donnée ;
set_count: met à jour le nombre de cases minées adjacentes à une case non minée.


# let initialize_board cf = 
   let cell_init () = { mined=false; seen=false; flag=false; nbm=0 } in 
   let copy_cell_init b (i,j) = b.(i).(j) <- cell_init() in
   let set_mined b n = b.(n / cf.nbrows).(n mod cf.nbrows).mined <- true
   in
   let count_mined_adj b (i,j) =
     let x = ref 0 in
     let inc_if_mined (i,j) = if b.(i).(j).mined then incr x 
     in List.iter inc_if_mined (neighbours cf (i,j)) ;
        !x
   in
   let set_count b (i,j) =
     if not b.(i).(j).mined 
     then b.(i).(j).nbm <- count_mined_adj b (i,j)
   in
   let list_mined = random_list_mines (cf.nbcols*cf.nbrows) cf.nbmines in 
   let board = Array.make_matrix cf.nbcols cf.nbrows (cell_init ()) 
   in iter_on_cell cf (copy_cell_init board) ;
      List.iter (set_mined board) list_mined ;
      iter_on_cell cf (set_count board) ;
      board ;;
val initialize_board : config -> cell array array = <fun>

Découverte

Durant une partie, lorsqu'un joueur découvre une case dont aucun voisin n'est miné, il sait qu'il peut découvrir toutes les cases adjacentes sans risque, et ainsi de suite tant qu'il découvre d'autres cases sans voisin miné. Afin de soulager le joueur de cette étape fastidieuse (phase du jeu n'entraînant pas la moindre réflexion), notre Démineur découvre lui-même toutes ces cases. Pour ce faire, nous écrivons la fonction cells_to_see qui renvoie la liste de toutes les cases à découvrir quand une case est ouverte.

L'algorithme est simple à exprimer : si la case découverte a des voisins minés alors la liste se résume à cette unique case; sinon, c'est l'ensemble de ses voisins plus les listes des cases à découvrir quand on découvre chacun des voisins. La difficulté est d'écrire un programme qui ne boucle pas car bien évidement une case est un voisin de son voisin. Il faut donc faire en sorte de ne pas examiner plusieurs fois les mêmes cases.
Pour garder une trace des cases examinées, on utilise le tableau de booléens visited. Il est de même dimension que le champ de mines, on y marque avec la valeur true qu'une case a déjà été examinée. On applique récursivement la recherche des cases à découvrir uniquement sur les cases non marquées.

On utilise la fonction auxiliaire relevant qui calcule, à partir de la liste des voisins d'une case deux sous-listes. Chacune de ces sous-listes ne contient que des voisins ni minés, ni déjà découverts, ni marqués par le joueur et ni déjà visités. La première sous-liste contient les voisins ayant au moins un voisin miné ; la seconde contient les voisins n'ayant pas de voisin miné. On en profite pour marquer comme visitées toutes ces cases. Remarquons que nous excluons les cases marquées par le joueur même si elles ne sont pas minées, car le sens de cette marque est d'interdire la découverte de la case.

La fonction locale cells_to_see_rec réalise la boucle récursive de recherche. Elle construit la liste des cases à découvrir et prend en argument la liste des cases à examiner qui est maintenue à jour. On démarre avec la liste contenant uniquement la dernière case découverte après l'avoir marquée comme visitée.


# let cells_to_see bd cf (i,j) = 
   let visited = Array.make_matrix cf.nbcols cf.nbrows false in 
   let rec relevant = function 
       [] -> ([],[])
     | ((x,y) as c)::l -> 
          let cell=bd.(x).(y)
          in if cell.mined || cell.flag || cell.seen || visited.(x).(y) 
             then relevant l
             else let (l1,l2) = relevant l 
                  in visited.(x).(y) <- true ;
                     if cell.nbm=0 then (l1,c::l2) else (c::l1,l2)
   in 
   let rec cells_to_see_rec = function 
       [] -> []  
     | ((x,y) as c)::l -> 
           if bd.(x).(y).nbm<>0 then c :: (cells_to_see_rec l)
           else let (l1,l2) = relevant (neighbours cf c)
                in  (c :: l1)  @  (cells_to_see_rec (l2 @ l))
   in visited.(i).(j) <- true ;
      cells_to_see_rec [(i,j)]  ;;
val cells_to_see :
  cell array array -> config -> int * int -> (int * int) list = <fun>

À première vue, l'argument de cells_to_seen_rec peut croître entre deux appels alors que la récurrence se fait sur cet argument. On peut donc se demander si cette fonction termine toujours ?
L'utilisation du tableau visited nous garantit qu'une case déjà marquée ne peut être dans le résultat de relevant. Or les cases venant augmenter la liste des cases à examiner proviennent toutes de relevant. De plus, cette fonction marque toutes les cases qu'elle renvoie. Ceci nous garantit qu'une case ne pourra être renvoyée qu'une seule fois par relevant donc n'être qu'une seule fois dans la liste des cases à examiner. Le nombre de cases possibles étant fini, il en découle que la fonction termine.

Ceci clôt la partie hors affichage du Démineur, profitons-en pour faire un point sur le style de programmation que nous avons adopté. Le choix de structures modifiables (tableaux et champs mutables) nous a imposé un style impératif utilisant des boucles et des affectations. Pourtant, pour traiter les problèmes auxiliaires nous avons fait usage de listes et les fonctions de traitement adoptent un style fonctionnel. En fait, le style de programmation nous a été dicté par les structures de données que nous souhaitions manipuler. Le cas de la fonction cells_to_seen est symptomatique de cela : c'est une fonction manipulant des listes, et il est apparu naturel d'adopter un style fonctionnel. Pourtant, nous utilisons un tableau pour identifier les cases déjà traitées et nous dérogeons à la fonctionnalité pour maintenir ce tableau. Nous aurions pu dans un pur style fonctionnel maintenir une liste des cases traitées et vérifier si une case apparaissait ou non dans cette liste. Mais le coût de cette méthode aurait été important (la recherche de la présence d'un élément est linéaire suivant la taille de la liste alors qu'avec un tableau elle est constante), et elle ne simplifiait pas le programme.

Affichage du jeu Démineur

Cette partie est dépendante des structures de données représentant l'état du jeu (voir page ??). Il s'agit principalement d'afficher les différents composants de la fenêtre du Démineur suivant la figure 6.6. On utilise pour cet affichage les fonctions sur les boîtes vues page ??.

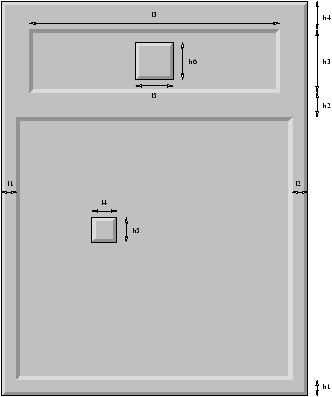
Figure 6.6 : La fenêtre principale du Démineur

Les paramètres suivants définissent les caractéristiques des différents composants de la fenêtre graphique.


# let b0 = 3 ;;
# let l1 = 15 ;;
# let l2 = l1 ;;
# let l4 = 20 + 2*b0 ;;
# let l3 = l4*default_config.nbcols + 2*b0 ;;
# let l5 = 40 + 2*b0 ;;


# let h1 = l1 ;;
# let h2 = 30 ;;
# let h3 = l5+20 + 2*b0 ;;
# let h4 = h2 ;;
# let h5 = 20 + 2*b0 ;;
# let h6 = l5 + 2*b0 ;;

Nous les utilisons pour étendre la configuration de base du démineur (valeur de type config). Nous définissons l'enregistrement window_config ci-dessous. Le champ cf contient la configuration minimale. On associe une boîte à chacun des composants de l'affichage : fenêtre globale (champ g_bcf), champ de mines (champ f_bcf), fenêtre de dialogue (champ m_bcf) avec deux sous boîtes (champs m1_bcf et m2_bcf), bouton de marquage (champ s_bcf), case courante (champ cc_bcf).


# type window_config = {
   cf : config ;            
   g_bcf : box_config ;   
   f_bcf : box_config ; 
   m_bcf : box_config ;
   m1_bcf : box_config ;
   m2_bcf : box_config ; 
   s_bcf : box_config ; 
   mutable cc_bcf : box_config ;
   cell : int*int -> (int*int) ;
   coor : int*int -> (int*int) 
 } ;;

De plus, une valeur de type window_config fournit deux fonctions :

cell : qui prend les coordonnées d'une case et rend les coordonnées de la boîte correspondante.
coor : qui prend les coordonnées d'un pixel de la fenêtre et rend les coordonnées de la case correspondante.

Configuration

On définit ensuite une fonction construisant une configuration graphique (de type window_config) en fonction d'une configuration minimale (de type config) et des paramètres définis plus haut. Les valeurs des paramètres de certains composants dépendent les uns des autres. Par exemple, la largeur de la boîte globale dépend de la largeur du champ de mines qui dépend à son tour du nombre de colonnes. Pour ne pas recalculer plusieurs fois une même valeur, nous renseignons incrémentalement les champs des composants. Cette phase d'initialisation d'un ensemble graphique est toujours un peu fastidieuse en l'absence de primitives ou d'outils adéquats.


# let make_box x y w h bw r =
   { x=x; y=y; w=w; h=h; bw=bw; r=r; b1_col=grey1; b2_col=grey3; b_col=grey2 } ;;
val make_box : int -> int -> int -> int -> int -> relief -> box_config =
  <fun>
# let make_wcf cf = 
   let wcols =  b0 + cf.nbcols*l4 + b0 
   and hrows =  b0 + cf.nbrows*h5 + b0  in
   let g_bcf =  let gw = (b0 + l1 + wcols + l2 + b0) 
                and gh = (b0 + h1 + hrows + h2 + h3 + h4 + b0)
                in make_box 0 0 gw gh b0 Top
   and f_bcf = make_box l1 h1 wcols hrows b0 Bot  in
   let m_bcf = make_box  ((g_bcf.w - l3) / 2) (b0+h1+hrows+h2) l3 h3 b0 Bot  in 
   let m1_bcf = make_box (m_bcf.x + b0) (b0 + h1 + hrows + h2)
                         ((l3-l5)/2-(2*b0)) (h3-(2*b0)) 5 Flat  in
   let s_bcf = make_box (m1_bcf.x + m1_bcf.w) 
                        (m1_bcf.y + (h3-h6) / 2) l5 h6 b0 Top  in 
   let m2_bcf = make_box (s_bcf.x + s_bcf.w) 
                         m1_bcf.y m1_bcf.w m1_bcf.h 5 Flat  in
   let cc_bcf = make_box 0 0 l4 h5 b0 Top
   in { cf = cf; 
        g_bcf = g_bcf; f_bcf=f_bcf; m_bcf=m_bcf; m1_bcf=m1_bcf; 
        s_bcf=s_bcf; m2_bcf=m2_bcf; cc_bcf = cc_bcf;
        cell = (fun (i,j) -> ( l1+b0+l4*i , h1+b0+h5*j)) ;
        coor = (fun (x,y) -> ( (x-l1)/l4 , (y-h1)/h5 )) } ;;
val make_wcf : config -> window_config = <fun>

Affichages des cases

Il s'agit maintenant de définir les fonctions réalisant l'affichage des cases dans les différents cas possibles. Une case pourra être ouverte ou fermée et pourra contenir ou non une information. On affichera toujours (la boîte de) la cellule courante de la configuration du jeu (champs cc_bcf).

Nous définissons donc deux fonctions modifiant la configuration de la cellule courante ; l'une la fermant, l'autre l'ouvrant.


# let close_ccell wcf i j =
   let x,y = wcf.cell (i,j) 
   in wcf.cc_bcf <- {wcf.cc_bcf with x=x; y=y; r=Top} ;;
val close_ccell : window_config -> int -> int -> unit = <fun>
# let open_ccell wcf i j =
   let x,y = wcf.cell (i,j) 
   in wcf.cc_bcf <- {wcf.cc_bcf with x=x; y=y; r=Flat} ;; 
val open_ccell : window_config -> int -> int -> unit = <fun>

Suivant la phase de jeu, nous serons amenés à afficher une information sur les cases. Nous définissons, pour chaque cas, une fonction particulière.

Affichage d'une case fermée :


# let draw_closed_cc wcf i j = 
  close_ccell wcf i j;
  draw_box wcf.cc_bcf ;;
val draw_closed_cc : window_config -> int -> int -> unit = <fun>

Affichage d'une case ouverte avec son compte de mines :


# let draw_num_cc wcf i j n =
   open_ccell wcf i j ;
   draw_box wcf.cc_bcf ;
   if n<>0 then draw_string_in_box Center (string_of_int n) 
                                   wcf.cc_bcf Graphics.white ;;
val draw_num_cc : window_config -> int -> int -> int -> unit = <fun>

Affichage d'une case contenant une bombe :


# let draw_bomb_cc wcf i j = 
   open_ccell wcf i j ;
   let cc = wcf.cc_bcf 
   in draw_box wcf.cc_bcf ;
      Graphics.set_color Graphics.black ; 
      Graphics.fill_circle (cc.x+cc.w/2) (cc.y+cc.h/2) (cc.h/3) ;;
val draw_bomb_cc : window_config -> int -> int -> unit = <fun>

Affichage d'une case minée et marquée :


# let draw_flag_cc wcf i j =
   close_ccell wcf i j ;
   draw_box wcf.cc_bcf ;
   draw_string_in_box Center "!" wcf.cc_bcf Graphics.blue ;;
val draw_flag_cc : window_config -> int -> int -> unit = <fun>

Affichage d'une case marquée à mauvais escient :


# let draw_cross_cc wcf i j =
  let x,y = wcf.cell (i,j) 
  and w,h = wcf.cc_bcf.w, wcf.cc_bcf.h in
  let a=x+w/4 and b=x+3*w/4 
  and c=y+h/4 and d=y+3*h/4 
  in Graphics.set_color Graphics.red ;
     Graphics.set_line_width 3 ;
     Graphics.moveto a d ; Graphics.lineto b c ; 
     Graphics.moveto a c ; Graphics.lineto b d ;
     Graphics.set_line_width 1 ;;
val draw_cross_cc : window_config -> int -> int -> unit = <fun>

En cours de jeu, le choix de la fonction d'affichage d'une case est réalisé par :


# let draw_cell wcf bd i j = 
   let cell = bd.(i).(j) 
   in match (cell.flag, cell.seen , cell.mined ) with 
          (true,_,_)  -> draw_flag_cc wcf i j
        | (_,false,_) -> draw_closed_cc wcf i j
        | (_,_,true)  -> draw_bomb_cc wcf i j
        | _           -> draw_num_cc wcf i j cell.nbm  ;;
val draw_cell : window_config -> cell array array -> int -> int -> unit =
  <fun>

Une fonction spécifique affichera l'ensemble des cases en fin de partie. Elle diffère légèrement de la précédente car toutes les cases sont considérées comme devant être découvertes. De plus, on signale d'une croix rouge les cases marquées à tort par le joueur.


# let draw_cell_end wcf bd i j = 
   let cell = bd.(i).(j) 
   in match (cell.flag, cell.mined ) with 
          (true,true) -> draw_flag_cc wcf i j
        | (true,false) -> draw_num_cc wcf i j cell.nbm; draw_cross_cc wcf i j
        | (false,true) -> draw_bomb_cc wcf i j
        | (false,false) -> draw_num_cc wcf i j cell.nbm ;;
val draw_cell_end : window_config -> cell array array -> int -> int -> unit =
  <fun>

Affichage des autres composants

L'état du mode marquage est matérialisé par une boîte en creux ou en relief contenant le mot ON ou OFF :


# let draw_flag_switch wcf on =  
   if on  then wcf.s_bcf.r <- Bot  else wcf.s_bcf.r <- Top ;
   draw_box wcf.s_bcf ;
   if on  then draw_string_in_box Center "ON" wcf.s_bcf Graphics.red
   else draw_string_in_box Center "OFF" wcf.s_bcf Graphics.blue ;;
val draw_flag_switch : window_config -> bool -> unit = <fun>

Au dessus du bouton de marquage, on affiche son rôle :


# let draw_mark_title wcf =
   let m = "Marquage" in 
   let w,h = Graphics.text_size m in
   let x = (wcf.g_bcf.w-w)/2 
   and y0 = wcf.m_bcf.y+wcf.m_bcf.h in
   let y = y0+(wcf.g_bcf.h-(y0+h))/2 
   in Graphics.moveto x y ;
      Graphics.draw_string m ;; 
val draw_mark_title : window_config -> unit = <fun>

Tout au long de la partie, le nombre de cases restant à découvrir et le nombre de cases marquées sont affichés dans la boîte de message, de part et d'autre du bouton de marquage.


# let print_score wcf nbcto nbfc =
   erase_box wcf.m1_bcf ;
   draw_string_in_box Center (string_of_int nbcto) wcf.m1_bcf Graphics.blue ;
   erase_box wcf.m2_bcf ;
   draw_string_in_box Center (string_of_int (wcf.cf.nbmines-nbfc)) wcf.m2_bcf 
    ( if nbfc>wcf.cf.nbmines then Graphics.red else Graphics.blue ) ;;
val print_score : window_config -> int -> int -> unit = <fun>

Pour dessiner le champ de mines initial, il faut dessiner (nombre de lignes) × (nombre de colonnes) fois une même case fermée. C'est toujours le même dessin, mais il peut être assez long à faire puisqu'il faut dessiner et remplir en plus d'un rectangle, quatre trapèzes. Pour accélérer cette initialisation, nous avons recours à la technique consistant à ne dessiner qu'une seule case, la capturer sous forme d'un bitmap et le reproduire à chaque emplacement d'une case.


# let draw_field_initial wcf = 
   draw_closed_cc wcf 0 0 ;
   let cc = wcf.cc_bcf  in 
   let bitmap = draw_box cc ; Graphics.get_image cc.x cc.y cc.w cc.h  in
   let draw_bitmap (i,j) = let x,y=wcf.cell (i,j) 
                           in Graphics.draw_image bitmap x y 
   in iter_on_cell wcf.cf draw_bitmap  ;;
val draw_field_initial : window_config -> unit = <fun>

En fin de partie, on découvre la totalité du champ de mines en marquant d'une croix rouge les cases marquées à mauvais escient :


# let draw_field_end wcf bd = 
   iter_on_cell wcf.cf (fun (i,j) -> draw_cell_end wcf bd i j)  ;;
val draw_field_end : window_config -> cell array array -> unit = <fun>

Enfin, la fonction principale d'affichage de début de partie ouvre le contexte graphique et affiche l'état initial des différents composants.


# let open_wcf wcf = 
   Graphics.open_graph ( " " ^ (string_of_int wcf.g_bcf.w) ^ "x" ^
                         (string_of_int wcf.g_bcf.h)               ) ;
   draw_box wcf.g_bcf ;
   draw_box wcf.m_bcf ;
   draw_flag_switch wcf false ;
   draw_box wcf.f_bcf ;
   draw_field_initial wcf ;
   draw_mark_title wcf ;
   print_score wcf ((wcf.cf.nbrows*wcf.cf.nbcols)-wcf.cf.nbmines) 0 ;;
val open_wcf : window_config -> unit = <fun>

Notons que toutes les primitives d'affichage sont paramétrées par une configuration graphique de type window_config. Le fait d'avoir procédé de la sorte les rend indépendantes des choix de disposition des éléments composant notre Démineur. Si nous souhaitons modifier cette disposition, le code reste utilisable tel quel, seule la configuration doit être mise à jour.

Interaction entre le programme et le joueur

Définissons les différentes possibilités offertes au joueur :

il peut cliquer sur la case de sélection pour changer de mode (découverte ou marquage),
ou cliquer sur l'une des cases pour la découvrir ou la marquer,
ou il peut appuyer sur la touche 'q' pour quitter le jeu.

Rappelons qu'un événement de Graphics (Graphics.event) doit être associé à un enregistrement (Graphics.status) contenant les informations courantes sur la souris et le clavier à l'instant où se produit l'événement. Une interaction souris peut avoir lieu soit sur le bouton de marquage, soit sur une case du champ de mines. Tout autre événement souris doit être ignoré. Afin de différencier ces événements souris, nous nous donnons le type :


# type clickon = Out | Cell of (int*int) | SelectBox  ;;

D'autre part, l'appui sur le bouton de la souris et son relâchement sont deux événements distincts. Pour qu'un clic soit valide, nous imposons que les deux événements aient eu lieu sur le même composant (bouton de marquage ou case du champ de mines).


# let locate_click wcf st1 st2 =
   let clickon_of st = 
     let x = st.Graphics.mouse_x and y = st.Graphics.mouse_y
     in if x>=wcf.s_bcf.x && x<=wcf.s_bcf.x+wcf.s_bcf.w && 
           y>=wcf.s_bcf.y && y<=wcf.s_bcf.y+wcf.s_bcf.h  
        then SelectBox
        else let (x2,y2) = wcf.coor (x,y)
             in if x2>=0 && x2<wcf.cf.nbcols && y2>=0 && y2<wcf.cf.nbrows
                then Cell (x2,y2) else Out
   in 
   let r1=clickon_of st1 and r2=clickon_of st2
   in if r1=r2 then r1 else Out ;;
val locate_click :
  window_config -> Graphics.status -> Graphics.status -> clickon = <fun>

Le coeur du programme est la boucle d'attente et de traitement des événements définie dans la fonction loop. Elle s'inspire de la fonction squel décrite à la page ??, mais spécifie mieux les types d'événement souris. Cette boucle est interrompue :

par appui de la touche q (ou Q) que l'on interprète comme la volonté du joueur de terminer la partie ;
lorsque le joueur découvre une case minée, auquel cas il a perdu ;
lorsque le joueur a découvert toutes les cases non minées, auquel cas il a gagné.

On rassemble dans le type enregistrement demin_cf les différentes informations utiles aux fonctions de traitement de l'interaction :


# type demin_cf = 
   { wcf : window_config; bd : cell array array;
     mutable nb_marked_cells : int; 
     mutable nb_hidden_cells : int;  
     mutable flag_switch_on : bool } ;;

Les champs correspondent à :

wcf : la configuration graphique ;
bd : le tableau de cellules ;
flag_switch_on : un booléen indiquant si le jeu est en mode marquage ou non ;
nb_marked_cells : le nombre de cases marquées ;
nb_hidden_cells : le nombre de cases non minées restant à découvrir ;

La boucle principale s'écrit de la manière suivante :


# let loop d f_init f_key f_mouse f_end = 
   try
     while true do 
       let st = Graphics.wait_next_event 
                  [Graphics.Button_down;Graphics.Key_pressed]  
       in if st.Graphics.keypressed  then f_key st.Graphics.key
          else let st2 = Graphics.wait_next_event [Graphics.Button_up] 
               in f_mouse (locate_click d.wcf st st2)
     done
   with Fin -> ();;
val loop : demin_cf -> 'a -> (char -> 'b) -> (clickon -> 'b) -> 'c -> unit =
  <fun>

Les fonctions d'initialisation, de fin et de gestion clavier sont fort simples.


# let d_init d () = open_wcf d.wcf          
 let d_end  () = Graphics.close_graph()
 let d_key c = if c='q' || c='Q' then raise Fin;;
val d_init : demin_cf -> unit -> unit = <fun>
val d_end : unit -> unit = <fun>
val d_key : char -> unit = <fun>

Par contre la fonction de gestion des événements souris nécessite l'utilisation de quelques fonctions auxiliaires :

mark_cell : réponse à un clic sur une case en mode marquage actif.
ending : fin du jeu. On découvre tout le champ de mines, on affiche un message indiquant victoire ou défaite et on attend un événement souris ou clavier quelconque pour fermer l'application.
reveal : réponse à un clic sur une case en mode découverte (i.e. mode marquage inactif)


# let mark_cell d i j =
   if d.bd.(i).(j).flag 
   then ( d.nb_marked_cells <- d.nb_marked_cells -1; 
          d.bd.(i).(j).flag <- false )
   else ( d.nb_marked_cells <- d.nb_marked_cells +1 ; 
          d.bd.(i).(j).flag <- true ) ;
   draw_cell d.wcf d.bd i j ;
   print_score d.wcf d.nb_hidden_cells d.nb_marked_cells;;
val mark_cell : demin_cf -> int -> int -> unit = <fun>

# let ending d str = 
   draw_field_end d.wcf d.bd ;
   erase_box  d.wcf.s_bcf ;
   draw_string_in_box Center str d.wcf.s_bcf Graphics.black;
   ignore(Graphics.wait_next_event 
            [Graphics.Button_down;Graphics.Key_pressed]);
   raise Fin;;
val ending : demin_cf -> string -> 'a = <fun>
# let reveal d i j = 
   let reveal_cell (i,j) = 
     d.bd.(i).(j).seen <- true ; 
     draw_cell d.wcf d.bd i j ;
     d.nb_hidden_cells <- d.nb_hidden_cells -1 
   in 
     List.iter reveal_cell (cells_to_see d.bd d.wcf.cf (i,j)) ;
     print_score d.wcf d.nb_hidden_cells d.nb_marked_cells ;
     if d.nb_hidden_cells = 0 then ending d "GAGNE";;
val reveal : demin_cf -> int -> int -> unit = <fun>

La fonction de traitement de l'événement souris filtre une valeur de type clickon.


# let d_mouse d click = match click with 
     Cell (i,j) -> 
       if d.bd.(i).(j).seen then ()
       else if d.flag_switch_on then mark_cell d i j 
       else if d.bd.(i).(j).flag then ()
       else if d.bd.(i).(j).mined then ending d "PERDU"
       else reveal d i j
   | SelectBox -> 
       d.flag_switch_on <- not d.flag_switch_on;
       draw_flag_switch d.wcf d.flag_switch_on
   | Out -> () ;;
val d_mouse : demin_cf -> clickon -> unit = <fun>

La création d'une configuration de jeu a besoin de trois paramètres : le nombre de lignes, le nombre de colonnes et le nombre de mines.


# let create_demin nb_c nb_r nb_m = 
   let nbc = max default_config.nbcols nb_c 
   and nbr = max default_config.nbrows nb_r in 
   let nbm = min (nbc*nbr) (max 1 nb_m) in
   let cf = { nbcols=nbc ; nbrows=nbr ; nbmines=nbm } in 
   generate_seed () ;
   let wcf = make_wcf cf in
   {  wcf = wcf ;
      bd = initialize_board wcf.cf;
      nb_marked_cells = 0; 
      nb_hidden_cells = cf.nbrows*cf.nbcols-cf.nbmines;
      flag_switch_on = false } ;;
val create_demin : int -> int -> int -> demin_cf = <fun>

La fonction de lancement crée une configuration à partir du nombre de colonnes, de lignes et de mines puis démarre la boucle principale de gestion des événements.


# let go nbc nbr nbm = 
   let d = create_demin nbc nbr nbm in
   loop d (d_init d) d_key (d_mouse d) (d_end);;
val go : int -> int -> int -> unit = <fun>

L'appel go 10 10 10 construit un jeu de la taille de celui de la figure 6.5.

Pour en faire plus

On peut faire de ce programme un exécutable autonome. Le chapitre 7 explique comment le faire. Une fois cela réalisé, il est pratique de pouvoir donner les tailles du jeu sur la ligne de commande. Le chapitre 8 décrit ce passage d'arguments et l'applique au démineur (voir page ??).

Un autre type de problème est de faire jouer la machine pour découvrir les mines. Pour cela il convient de savoir déterminer un coup sûr et de le jouer en priorité, puis de calculer les probabilités de présence d'une mine pour chaque case et de jouer la case de plus faible probabilité.