DIY fast random tree generation


(ns my.m$macros)
(require '[reagent.core :as r])
(require '[reagent.ratom :as ratom])

DIY fast random tree generation

Berlin - Feb 24, 2018


;; A live-coding presentation made with klipse
;; (thank you Yeonathan/viebel!)
(defn showme [s] [:h3 (str s)])
[:div (showme (js/Date.))]

Who am I? frederic.peschanski@lip6.fr — fredokun @ github

associate professor at Sorbonne University (ex-UPMC)
researcher at the Lip6 computer science laboratory
(live) programming & maths geek
long-time Lisper (scheme, CL, clojure(script))

⇒ Clojure as a proof assistant: The LaTTe project @ github (shameless plug!)

This talk

Goals:

discuss a hot topic in Clojure: random generation
show some beautiful maths (combinatorics)…

… through (hopefully) intelligible and interactive clojure(script)

⇒ no greek letters !

Non-goals:

yet another test.check tutorial (cf. the excellent talk at Conj'17)
an academic lecture (not sure, you tell me)

Thanks to:

Antoine Genitrini and Mathieu Dien for the trickiest maths part
Yeonathan Sharvit (viebel) for klipse
Clojure Paris Meetup and Hiram Madelaine for shepherding

Agenda

Random generation: arts & crafts
Generating binary trees and (then) general trees
A generic generator based on Bolzmann sampling

Warning ! this presentation is code heavy! The whole source code is in the slides,
we’ll need to skip some parts (but you can play with the whole bunch online…)

Random generation: check-list

Hanna wants to generate some objects at random

Important questions for Hanna:

What kind of randomness ?
→ truely random: non-determinism, unpredictability, non-reproducibility
→ pseudo random: determinism, predictability, reproducibility

What is the distribution of the objects to generate?
→ unbiased sampling: uniform distribution according to a given notion of size
→ biased sampling: following a given statistical distribution
→ don’t know (don’t care?) sampling

Characteristics ?
→ expected sizes: small or large objects?
→ statistical quality: periodicity, etc.
→ performances: arithmetic complexity, memory usage, random-bit complexity (save the random bits!)

The random source …

It all starts with a good random source. For data generation we’ll
go a long way with a good Pseudo Random Number Generator (PRNG).

(https://xkcd.com/221/)

Question: a good (portable) PRNG for clojure/script?
(goodness: uniformity, reproducibilty, efficiency)

⇒ (defn xkcd-random-number [] 4)?
⇒ rand-cljc?
⇒ test.check?
⇒ a better source?

Random numbers in test.check

(require '[clojure.test.check.random
         :refer [make-random  ;; create source with seed
	         split        ;; two generators from one
		 rand-double  ;; uniform double in range [0.0;1.0[
		 rand-long    ;; uniform long (64 bits java, js ?)
		 ]])

(def src (make-random 424242))

(let [[src' src''] (split src)] ;; XXX: why two? we need only one ...
  [(rand-double src) (rand-double src') (rand-double src'')])
""

Incremental random generators

;; generate a double between 0.0 (inclusive) and 1.0 (exclusive)
(defn next-double [src]
  (let [[src' src''] (split src)] ;; XXX: throw src?
    [(rand-double src') src'']))

(next-double src)

""

;; generate an integer in some range
(defn next-int [src mini maxi]
  (let [[x src'] (next-double src)]
    [(int (+ (* (- maxi mini) x)
             mini)) src']))

(next-int src 24 450)
""

;; coin flips
(defn next-bool [src]
  (let [[x src'] (next-double src)]
    [(< x 0.5) src']))  ;; XXX: random bits leak !

(next-bool src)
""

Generating trees: why?

Why ?
- trees everywhere:
→ elements/compounds (files/directories, shapes/groups,…)
→ structured documents (sections/subsections,…)
→ tree-shaped datastructures
→ expression trees (generating programs?),
→ etc.
- a non-trivial case study for uniform random generation
- beautiful maths and algorithms

Generating trees: how?

How ?
- "simple" ad hoc algorithms for specific cases: binary trees and general trees
- more complex generic algorithms:
→ recursive generation (uniform, exact size, ≅ 10.000 nodes, not beautiful)
→ bolzmann sampling (uniform, approx size, ≅ 1.000.000 nodes, beautiful)

Binary trees

(require '[clojure.spec :as s])

;; a spec for binary trees (with keyword labels)
(s/def ::bintree
  (s/or :tip nil?
        :node (s/tuple ::label ::bintree ::bintree)))
(s/def ::label int?)

;; example
(def ex-btree [1,
               [2 nil nil],
               [3 [4 nil,
                   [5 nil nil]],
               [6 nil nil]]])

(s/valid? ::bintree ex-btree)
""

Random generation from spec (via test.check):

(require '[clojure.test.check.generators :as gen])

(gen/generate (s/gen ::bintree) 10)
""

Observations
- non-uniform generation (it’s biased but don’t know how)
- lack of control: biased towards (very) small trees

Generating binary trees with test.check

Let's try the dedicated support for recursive structures

(def node-gen (fn [inner-gen]
                (gen/tuple gen/int inner-gen inner-gen)))

(def bt-gen (gen/recursive-gen node-gen (gen/return nil)))

(gen/generate bt-gen 10)
""

Observations
- non-uniform generation (it’s biased but don’t know how)
- lack of control: small-ish trees

Uniformity?

Unbiased sampling means sampling in the uniform distribution.

Defined for a combinatorial class:

each object has a finite size n
there is a finite number Cn of objects of a given size
uniform distribution: the probability of sampling an object of size n
is (/ 1.0 Cn)

Binary trees as a combinatorial class:

the size n of a tree is its number of (internal) nodes
but what about Cn?
⇒ Catalan numbers

Catalan numbers: counting binary trees

;; a point = a node or a tip (a `nil`)
(defn nb-points [n] (+ (* 2 n) 1))

;; a tip = a `nil` value
(defn nb-tips [n] (inc n))

;; counting binary trees (https://oeis.org/A000108)
(defn catalans
  ([] (cons 1 (cons 1 (catalans 1 1))))
  ([n Cn] (lazy-seq (let [Cn+1 (* (/ (* 2 (nb-points n))
                                     (nb-tips (inc n)))
	        		Cn)]
		    (cons Cn+1 (catalans (inc n) Cn+1))))))

(take 10 (catalans))
""

nil ;; tree of size 0

A beautiful bijection

<academic-stuff>

</academic-stuff>

The generation algorithm

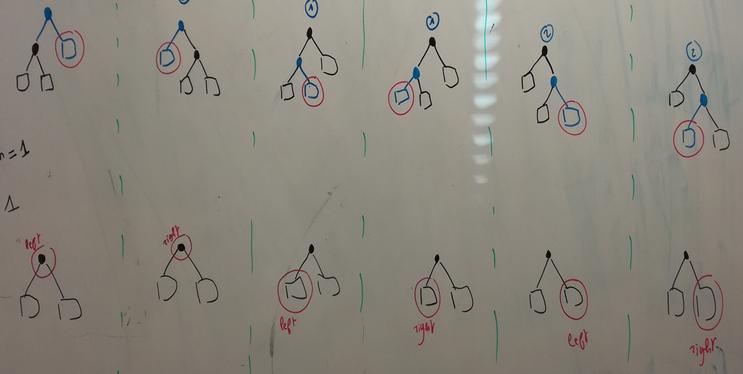
Incremental generation of a binary tree uniformly at random
(a.k.a. Remy algorithm)

Input: a tree of size n taken uniformly at random
i.e. obtained with probabilty (/ 1.0 (nth (catalans) n))

Example: [1 [2 nil nil] [3 nil nil]]

Step 1: we pickup a "point" (either a node or a nil) uniformly at random
⇒ we need a random integer between 0 and (* 2 n)
Example: we pickup the 4th point: [1 [2 nil <nil>] [3 nil nil]]

Step 2: We select a direction, either left or right
⇒ We need a random boolean (coin flip)
Example: :left

Step 3: We build the tree of size n+1 according to the bijection, and remove the "mark"
Example: [1 [2 nil [4 <nil> nil]] [3 nil nil]]

Finally, the generated tree is: [1 [2 nil [4 nil nil]] [3 nil nil]]

⇒ this tree has been taken with probability (/ 1.0 (nth (catalans) (inc n)))
(proof is easy thanks to the bijection… but let’s skip it)

Tree representation

Step 1 (pickup a "point") is O(n) if we use the "classical" representation of binary trees.

⇒ Alternative "vectorized" representation to achieve "almost" O(1)

(defn root [lbl]
  [[lbl nil 1 2] #{0} #{0}])

(defn append-leaf [vtree lbl parent side]
  (let [[_ _ pleft pright] (nth vtree parent)
        pside (if (= side :left) pleft pright)
        tip-idx (count vtree)]
    [(-> vtree
       (assoc pside [lbl parent tip-idx (inc tip-idx)])
       (conj #{pside} #{pside})) pside]))

;; representation of [:a nil nil]
(root :a)
""

;; [:a [:b nil nil] nil]
(-> (root :a)
    (append-leaf :b 0 :left))
""

;; [:a [:b nil [:c nil nil]] nil]
(-> (root :a)
    (append-leaf :b 0 :left) (first)
    (append-leaf :c 1 :right))
""

From classical to vectorized binary trees

;; remark: tail-recursive
(defn vbuild
  ([t]
   (if-let [[lbl left right] t]
     (vbuild (root lbl) 0 :left left (list [0 :right right]))
     []))
  ([vtree parent side t cont]
   ;; a node
   (if-let [[lbl left right] t]
     (let [[vtree' nparent] (append-leaf vtree lbl parent side)]
       (recur vtree' nparent :left left (cons [nparent :right right] cont)))
     ;; a nil
     (if-let [[[parent' side' t'] & cont'] cont]
       (recur vtree parent' side' t' cont')
       vtree))))

(vbuild [:a [:b nil nil] nil])
""

Interlude: folding vectorized trees

;; the root is the only node with a  `nil` parent
(defn search-root [vtree]
  (loop [vtree vtree, idx 0]
    (if (seq vtree)
      (if (and (vector? (first vtree))
               (nil? (second (first vtree))))
        idx
        (recur (rest vtree) (inc idx)))
      ;; not found
      nil)))

;; a tail-recursive folder for vtrees
;; (let's skip the details...)
(defn vfold
  ([f init vtree]
   (let [root-idx (search-root vtree)]
     (vfold f init root-idx vtree '())))
  ([f init node-idx vtree cont]
   (cond
     (int? node-idx)
     (let [node (nth vtree node-idx)]
       (if (vector? node)
         (let [[lbl _ left-idx right-idx] node]
           (recur f init left-idx vtree (cons [::right lbl init right-idx] cont)))
         ;; tip
         (recur f init nil vtree cont)))
     ;; continuation (tail-recursion)
     (seq cont)
     (case (ffirst cont)
       ::right (let [[_ lbl racc right-idx] (first cont)]
                 (recur f racc right-idx vtree (cons [::finish lbl init] (rest cont))))
       ::finish (let [[_ lbl lacc] (first cont)]
                  (recur f (f lbl lacc init) nil vtree (rest cont))))
     :else ;; no more continuation
     init)))

(vfold #(+ 1 %2 %3) 0 (vbuild [:a nil [:b [:c nil [:d nil nil]] [:e nil nil]]]))
""

From vectorized to classical binary trees

;; typical fold one-liner
(defn vunbuild [vtree]
  (vfold vector nil vtree))

(vbuild [:a [:b nil nil] [:c nil nil]])
""

Apply the bijection = "Grafting"

Code size alert: grafting has several subcases
(let’s skip the details…)

(defn reparent [vtree parent old-child new-child]
  (update vtree parent (fn [[plbl pparent pleft pright]]
                         (if (= pleft old-child)
                           [plbl pparent new-child pright]
                           [plbl pparent pleft new-child]))))

(defn newchild [lbl parent side other new]
  (case side
    :left [lbl parent other new]
    :right [lbl parent new other]))

(defn graft [vtree lbl where side]
  (let [wnode (get vtree where)
        graft-idx (count vtree)]
    (if (vector? wnode)
      ;; <<either a node>>
      (let [[wlbl wparent wleft wright] wnode]
        ;; node case
        (as-> vtree $
            (if wparent (reparent $ wparent where graft-idx) $)
            (assoc $ where [wlbl graft-idx wleft wright])
            (conj $ (newchild lbl wparent side where (inc graft-idx))
                  #{graft-idx})))
      ;; <<or else a tip>>
      (let [parent (first wnode)]
        (-> vtree
            (reparent parent where graft-idx)
            (assoc where #{graft-idx})
            (conj (newchild lbl parent side where (inc graft-idx))
                  #{graft-idx}))))))
""

Grafting examples

(vunbuild (root :a))
""

(root :a)
""

(vunbuild (-> (root :a)
              (graft :b 0 :left)))
""

The random generation algorithm

(defn rand-bintree [src nb size vtree]
  (if (= nb size)
    [vtree src]
    (let [;; step 1: pickup a "point"
          [pos src'] (next-int src 0 (dec (count vtree)))
	  ;; step 2: choose side: left (true) or right (false)
          [left src''] (next-bool src')]
      (recur src'' (inc nb) size
             ;; step 3: apply bijection
             (graft vtree (keyword (str (inc nb))) pos (if left :left :right))))))

(rand-bintree (make-random 424242) 1 20 (root :1))
""

Observations
- uniform generation (we’ll see)
- controllable: the size parameter … is … the size of the tree
- efficient: generate quite large trees (linear time algo, tail-recursive)

Uniformity?

The theory (analytic combinatorics) gives an asymptotic for the average height of binary trees.

(defn avg-height-theory [size]
  (* 2.0 (Math/sqrt (* Math/PI size))))

(avg-height-theory 1000)
""

Let’s check this …

(defn vheight [vtree]
  (vfold #(+ 1 (max %2 %3)) 0 vtree))

(defn rand-bintrees [src size]
  (lazy-seq (let [[vtree src'] (rand-bintree src 1 size (root :1))]
               (cons vtree (rand-bintrees src' size)))))


(defn avg-height-practice [seed nb size]
  (/ (reduce + 0 (map vheight (take nb (rand-bintrees (make-random seed) size))))
     nb))

;; (time (avg-height-practice 14922 50 1000))
""

General trees

(s/def ::gentree (s/tuple keyword? (s/coll-of ::gentree :kind vector?)))

(def ex-rtree [:1 [[:2 [[:3 []]
                        [:4 [[:5 [[:6 []]]]]]]]
                   [:7 []]
                   [:8 [[:9 []]
                        [:10 []]
                        [:11 []]
                        [:12 []]]]]])

(s/valid? ::gentree ex-rtree)

Uniform random generation of general trees?

From binary to general trees (and vice-versa)

Yet another bijection.

<academic-stuff>

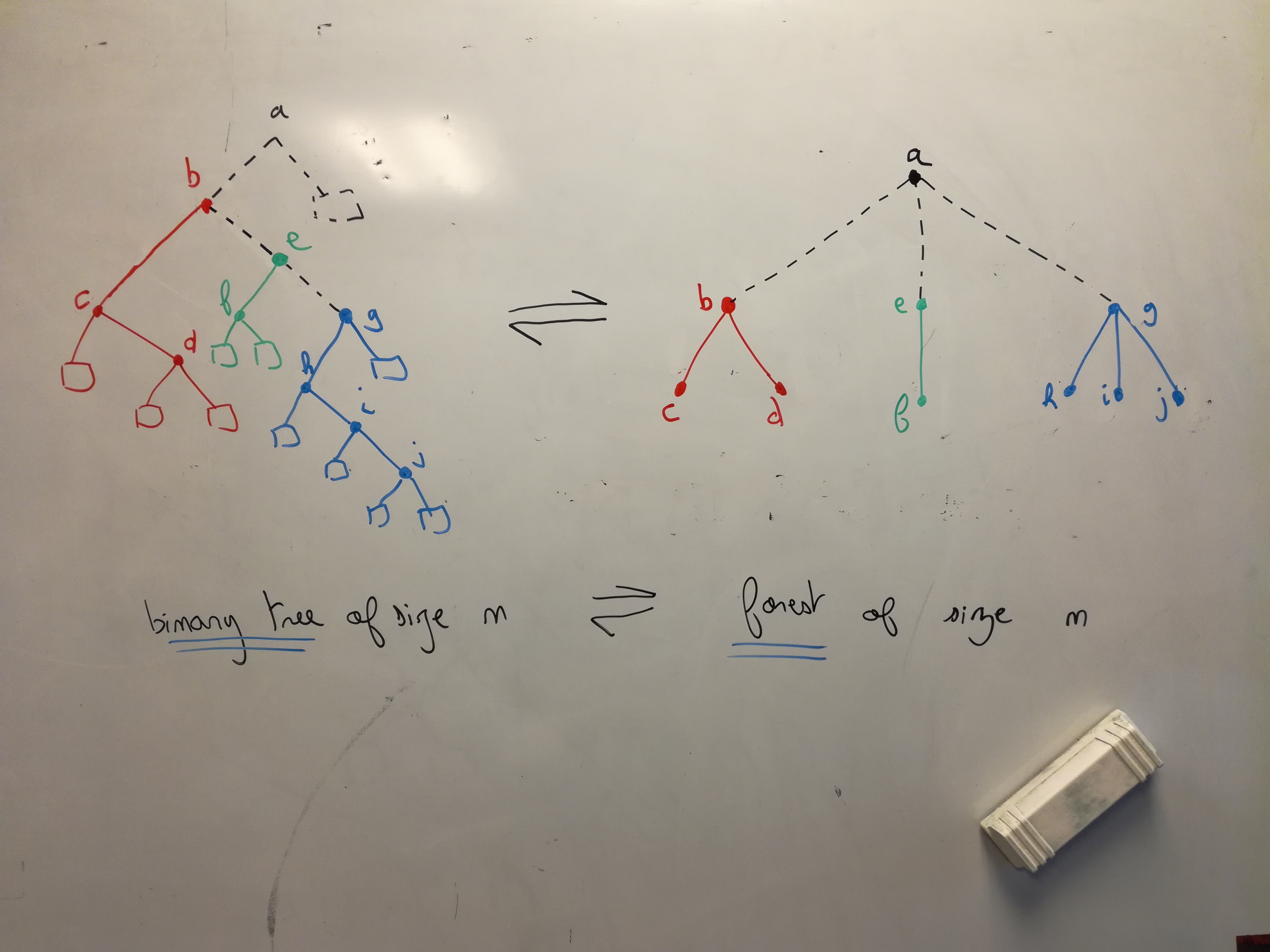
</academic-stuff>

Random generation of general trees

Step 1 : generate a binary tree uniformly at random (size n)

(def mybtree (-> (rand-bintree (make-random 424242) 1 10 (root :1))
                 (first)
		 (vunbuild)))

mybtree
""

Step 2 : convert it to a forest (size n)

(defn btree->forest [bt]
  (if (nil? bt)
    '()
    (let [[lbl left right] bt
          lefts (btree->forest left)
          rights (btree->forest right)]
      (cons [lbl (into [] lefts)]
            rights))))

(btree->forest mybtree)
""

Step 3 : add a root to obtain a general tree (size n+1)

(def mygtree [:0 (into [] (btree->forest mybtree))])

mygtree
""

Observation
- the forest is generated uniformly for size n
- the general tree is generated uniformly for size n+1
(there is only one way to put the root node)

The uniform random generator for general trees

(defn rand-gentree [src size]
  (let [;; step 1 : generate a binary tree uniformly at random
         [vtree src'] (rand-bintree src 1 size (root :1))
          btree (vunbuild vtree)
          ;; step 2 : convert to a forest
         forest (btree->forest btree)
          ;; step 3 : add a root
         gtree [:0 (into [] forest)]]
   [gtree src']))

(first (rand-gentree (make-random 424242) 20))
""

Generic tree-generation algorithms ?

The generation of binary trees and (then) general trees is a good
start but we often encounter more complex tree structures based
on a grammar.

Question: is it possible to build a generator from a grammar?

no generic bijection for trees of size n and trees of size n+1
(i.e. the binary tree bijection does not "scale")

a rather complex algorithmic framework exists for exact size generation:
the recursive method

a much simpler algorithm family for approximate size generation:
boltzmann sampling

Remark: the recursive method and boltzmann sampling are both
based on analytic combinatorics and tightly related to
the average-case complexity analysis of algorithms.

Tree grammars

We spec a simple (map-based) DSL for tree grammars.

(s/def ::neutral #{1}) ;; ≅ empty
(s/def ::atom #{'z})   ;; an atom has size 1
;; (+ <e1> <e2> ...) either ... or ...
(s/def ::sum (s/cat :sum #{'+} :elems (s/+ ::elem)))
;; (* <e1> <e2> ...) tupling
(s/def ::prod (s/cat :prod #{'*} :elems (s/+ ::elem)))
;; recursion
(s/def ::ref keyword?)

(s/def ::elem (s/or :neutral ::neutral
                    :atom ::atom
                    :sum ::sum
                    :prod ::prod
                    :ref ::ref))

(s/def ::grammar (s/map-of keyword? ::elem))
""

Example 1: binary trees

(def bt-gram '{:btree (+ :tip (* z :btree :btree))
               :tip 1})

(s/valid? ::grammar bt-gram)

Example 2: general trees

(def gt-gram '{:gtree (* z :forest)
               :forest (+ 1 (* :gtree :forest))})

(s/valid? ::grammar gt-gram)

Non-trivial tree grammars

Example:

(def tt-gram '{:ttree (+ 1 :two :three)
               :two (* z :ttree :ttree)
	       :three (* z z :ttree :ttree :ttree)})

(s/valid? ::grammar tt-gram)

In english: trees with internal nodes of arity either 2 and 3,
such that the ternary nodes have size 2 and binary nodes size 1.

⇒ how to generate such trees uniformly at random?

From tree grammars to generating functions

The tree grammars look suspiciously like equations…

'{:btree (+ :tip (* z :btree :btree))
  :tip 1}
""

Functional equation: btree(z) = 1 + z * btree(z) * btree(z)

btree(z) is called a generating function, it is a power series of the form:

(* (coef n) (Math/pow z n)) for n in (range)

where n is the size of the generated objects, and (coef n) the number
of such objects. For binary trees it’s the Catalan numbers we’ve already seen.

(take 15 (catalans))

What the underlying maths tell us about the generating functions
corresponding to tree grammars:
- they converge (i.e. are analytic) in 0
- there exists a radius of convergence between 0 (inclusive) and 1.0 (exclusive)
the limit point is called the (main) singularity

Boltzman probability

Suppose we have a tree grammar C
The Boltzmann probabilty of an object c generated by this grammar is:

(/ (Math/pow z (size-of c)) (C z))

the z is the Boltzmann parameter
(C z) is the evaluation of the functional equation at that parameter.

Remark: because of recursion, we need to bootstrap the evalution somehow…

(defn eval-elem [elem z weights]
  (cond
    (= elem 1) 1.0
    (= elem 'z) z
    (keyword? elem) (get weights elem)
    :else (let [[op & args] elem]
      (case op
        + (apply + (map #(eval-elem % z weights) args))
        * (apply * (map #(eval-elem % z weights) args))))))

(eval-elem '(* z :btree :btree) 0.25 {:btree 2.0, :tip 1.0})
""

(defn mapkv [f m]
  (into {} (map (fn [[k v]] (f k v)) m)))

(defn eval-grammar [grammar z weights]
  (mapkv (fn [ref elem] [ref (eval-elem elem z weights)]) grammar))

(eval-grammar bt-gram 1.0 {:btree 0.0 :tip 0.0})
""

Boltzmann sampling

Sampling of an object with a Boltmann model C of parameter z:

if C is 1 (a constant) then return the empty object (of size 0)
if C is z (an atom) then return the corresponding object of size 1
if C is (+ A B) (disjoint sum) then:
⇒ return an object of A with probability (/ (A z) (B z))
⇒ otherwise return an object of B
if C is (* A B) generate a pair [a b] with a an object of A and b an object of B

Questions:
- what should be the value of z?
- how to compute the probabilities for disjoint sums?

Singular sampling

The singularity is the limit of convergence for the generating functions

Theorem: By choosing the singularity as the Bolzmann parameter,
the expect size of an object generated by a Boltmann sampler is infinite.

Singular Boltzmann sampling = generating objects near or at the singularity.

Question: how to find the singularity for a given tree grammar?

⇒ numerical computation

Singularity oracle

(declare iter)     ;; newton iteration
(declare diverge?) ;; divergence (we went too far)

;; Mr Oracle, please find the singularity
(defn oracle [class zmin zmax eps-iter eps-div]
  ;; (println "[search] zmin=" zmin "zmax=" zmax)
  (if (< (- zmax zmin) eps-iter)
    [zmin (iter class zmin eps-div true)]
    (let [z (/ (+ zmin zmax)
               2.0)
          v (iter class z eps-div false)]
      (if (diverge? v eps-div)
        (recur class zmin z eps-iter eps-div)
        (recur class z zmax eps-iter eps-div)))))


;; (oracle tt-gram 0.0 1.0 0.00001 0.00000001)

;; (oracle bt-gram 0.0 1.0 0.001 0.000001)

""

The (numerical) details

;; distance between vectors v1 and v2
(defn norm [v1 v2]
  (reduce-kv (fn [norm elem y1]
               (let [y2 (get v2 elem)
                     y (Math/abs (- y1 y2))]
                 (if (> y norm) y norm))) 0.0 v1))

(norm {:a 0.1 :b 0.3} {:a 0.2 :b -0.2})
""

;; iteration until distance is less than `eps` (thank you Mr. Newton)
(defn iter [gram z eps debug]
  (loop [v1 (mapkv (fn [k _] [k 0.0]) gram)]
    (let [v2 (eval-grammar gram z v1)]
      ;; (when debug (println "[iter] v2=" v2 "norm=" (norm v1 v2)))
      (if (<= (norm v1 v2) eps)
        v2
        (recur v2)))))

;; (oracle bt-gram 0.0 1.0 0.001 0.01)
""

(defn some-kv [pred m]
  (reduce-kv (fn [res k v]
               (let [r (pred k v)]
                 (if r
                   (reduced r)
                   res))) nil m))

;; vector has diverged wrt. eps?
(defn diverge? [v eps]
  (some-kv (fn [_ w] (or (< w 0.0) (> w (/ 1.0 eps)))) v))

""

Weighted grammars

An interesting pre-computation is to calculate the weights for
the difference branches of disjoint sums (+ operator)

(defn weighted-args [args z weights]
  (let [eargs (mapv (fn [arg] [arg (eval-elem arg z weights)]) args)
        total (apply + (map second eargs))]
    (loop [eargs eargs, acc 0.0, wargs []]
      (if (seq eargs)
        (let [[arg weight] (first eargs)
              acc' (+ acc weight)]
          (recur (rest eargs) acc' (conj wargs [arg (/ acc' total)])))
        ;; no more arg
        wargs))))

(defn weighted-elem [elem z weights]
  (cond
    (#{1 'z} elem) elem
    (keyword? elem) elem
    :else (let [[kind & args] elem]
            (case kind
              * elem
              + (cons '+ (weighted-args args z weights))))))

(defn weighted-gram [class z weights]
  (mapkv (fn [ref elem] [ref (weighted-elem elem z weights)]) class))


(let [[z v] (oracle tt-gram 0.0 1.0 0.00001 0.00000001)]
  (weighted-gram tt-gram z v))

tt-gram

""

Non-deterministic choice

(defn choose [src choices]
  (reduce (fn [[src res] [elem proba]]
            (let [[x src'] (next-double src)]
              (if (<= x proba)
                (reduced [src' elem])
                [src' res]))) [src nil] choices))


(choose (make-random) [[1 0.2] [:ttree 0.8] [:two 1.0]])
""

Boltzmann sampler

Based on the weighted grammer, the random generator is very simple.

(defn gentree [src wgram label elem]
  (cond
    (= elem 1) nil
    (= elem 'z) 'z
    (keyword? elem) (recur src wgram elem (get wgram elem))
    :else (let [[op & args] elem]
      (case op
        + (let [[src' choice] (choose src args)]
            (gentree src wgram label choice))
        * (into [label] (filter #(not (#{1 'z} %)) (map #(gentree src wgram label %) args)))))))


(gentree (make-random)
         '{:three (* z z :ttree :ttree :ttree),
           :two (* z :ttree :ttree),
           :ttree (+ [1 0.5565458972998509] [:two 0.8892848135820887] [:three 1])} :ttree :ttree)

""

Problem: the generated tree maybe very small (like nil) or very (very very …) large because
- the distribution of trees is relatively flat
- the expected size is infinite

Generation of size

;; (tail recursive) generation of size
(defn gensize
  [src wgram maxsize elem]
   (loop [src src, elem elem, size 0, cont '()]
     (if (>= size maxsize)
       [-1 src]
       (cond
         (nil? elem) (if (seq cont)
                        (recur src (first cont) size (rest cont))
                        [size src])
         (= elem 1) (recur src nil size cont)
         (= elem 'z) (recur src nil (inc size) cont)
	 (keyword? elem) (recur src (get wgram elem) size cont)
	 :else
         (let [[op & args] elem]
           (case op
             + (let [[src' elem'] (choose src args)]
                 (recur src' elem' size cont))
             * (recur src (first args) size (concat (rest args) cont))))))))


(gensize (make-random)
         '{:three (* z z :ttree :ttree :ttree),
           :two (* z :ttree :ttree),
           :ttree (+ [1 0.5565458972998509] [:two 0.8892848135820887] [:three 1])} 1000 :ttree)
""

Problem: many trees are small, the random source must be "heated" to
obtain better results

Heating the source

(defn gensizes [src wgram maxsize elem]
  (let [[size src'] (gensize src wgram maxsize elem)]
    (if (> size 0)
      (lazy-seq (cons [size src] (gensizes src' wgram maxsize elem)))
      (recur src' wgram maxsize elem))))

(take 30 (map first
  (gensizes (make-random 424242)
           '{:three (* z z :ttree :ttree :ttree),
             :two (* z :ttree :ttree),
             :ttree (+ [1 0.5565458972998509] [:two 0.8892848135820887] [:three 1])} 1000 :ttree)))
""

Really heating the source !

(take 10 (filter (fn [[size _]] (> size 100))
  (gensizes (make-random 424242)
           '{:three (* z z :ttree :ttree :ttree),
             :two (* z :ttree :ttree),
             :ttree (+ [1 0.5565458972998509] [:two 0.8892848135820887] [:three 1])} 1000 :ttree)))
""

The Boltzmann sampler (at last)

(defn boltzmann [src gram elem min-size max-size eps-iter eps-div]
  (let [;; (1) find the singularity and value of the genfun
        [z weights] (oracle gram 0.0 1.0 eps-iter eps-div)
	;; (2) precompute the weighted grammar
        wgram (weighted-gram gram z weights)
	[_ src'] (first (filter (fn [[size _]] (>= size min-size))
	                  (gensizes src wgram max-size elem)))]
    (gentree src' wgram elem elem)))

;; (boltzmann (make-random 424242) tt-gram :ttree 100 1000 0.001 0.0000001)
""

AAAAaaarrrrggggghhhhh!: gentree stack overflows… of course!

Tree generation (tail recursive)

(defn gentree' [src wgram maxsize elem]
  (loop [src src, label elem, elem elem, size 0, cont '()]
    ;; (println "label=" label "elem=" elem "size=" size "cont=" cont)
    (cond
      (>= size maxsize) [nil src]
      (keyword? elem) (recur src elem (get wgram elem) size cont)
      (= elem 1) (recur src nil nil size cont)
      (seq? elem)
      (let [[op & args] elem]
        (case op
          + (let [[src' elem'] (choose src args)]
              (recur src' label elem' size cont))
          * (recur src label (first args) size (cons [label (rest args)] cont))))
      :else
      (let [[[node rst] & cont'] cont]
        (cond
          (= elem 'z) (if (vector? node)
                        (recur src nil nil (inc size) cont)
                        (recur src nil nil (inc size) (cons [[node] rst] cont')))
          (nil? elem)
          (cond
            (seq rst) (recur src nil (first rst) size (cons [node (rest rst)] cont'))
            (seq cont')  (let [[[node' rst'] & cont''] cont']
                           (recur src nil nil size (cons [(conj node' node) rst'] cont'')))
            :else node))))))

A generic uniform random tree generator (finally…)

(defn boltzmann' [src gram elem min-size max-size eps-iter eps-div]
  (let [;; (1) find the singularity and value of the genfun
        [z weights] (oracle gram 0.0 1.0 eps-iter eps-div)
	;; (2) precompute the weighted grammar
        wgram (weighted-gram gram z weights)
	[_ src'] (first (filter (fn [[size _]] (>= size min-size))
	                  (gensizes src wgram max-size elem)))]
    (gentree' src' wgram max-size elem)))


;; (boltzmann' (make-random 424242) tt-gram :ttree 5 10 0.001 0.0000001)
""

Wrapup

random generation is (beautiful) science, art, and craft
unbiased sampling should be the default (bias should be an extra-ingredient)
better automated testing is possible
… the missing part: generation by recursive method

Thank you, Clojurian fellows!

← →

DIY fast random tree generation